As stated previously, most small bearings are used in applications where rotational accuracy and low torque are primary requirement and loads are light. Therefore the operating lifetime of the bearing is relatively long, and, if properly operated, failure is rare. Nevertheless, all bearings have a finite life under use and will eventually fail to perform satisfactorily due to an increase in noise and vibration, loss of running accuracy, deterioration of lubricant, or fatigue flaking of the rolling surfaces. Such failure modes are considered “normal” and can be predicted using standardized techniques.
In addition to normal deterioration, bearings may fail due to heat seizure, fracture, scoring of the rings and other conditions caused by improper use, selection or maintenance of the bearing. Such failures are not normal and can only be avoided by careful handling and correct operation of the bearing in a given application. |
BASIC BEARING FATIGUE LIFE |
| The basic fatigue life of a rotating deep-groove ball bearing is given as: |
|
|
|
|
3 |
. |
106 |
revolutions |
L10= |
|
where: |
L10 |
= |
rated fatigue life with a statistical reliability of 90% |
|
P |
= |
bearing equivalent load |
|
C |
= |
basic radial dynamic load rating (see individual bearing selection charts) |
|
| TEMPERATURE CORRECTION FACTOR |
If rolling bearings are used at high temperature, the hardness of the bearing steel decreases. Consequently the basic radial dynamic load rating C must be corrected:
Ct = ft • C
Bearing temperature oC |
< 150 |
175 |
200 |
250 |
Temperature factor ft |
1.00 |
0.95 |
0.9 |
0.75 |
Note: The temperature correction factor assumes that a lubricant is used that is suitable for given temperature. |
| GENERAL FATIGUE LIFE CORRECTION FACTORS |
The L10 preload life of a bearing is normally adjusted as follows, according to real-world operating conditions:
Lna |
= |
a1a2 L10 |
where: |
Lna = adjusted bearing fatigue life |
|
a1 = Life correction factor for material and desired statistical reliability, the values for a1 being given below:
Values for Life Correction Factor a1
MATERIAL |
STATISTICAL RELIABLITY (%) |
90 |
95 |
96 |
97 |
98 |
99 |
52100 |
1.00 |
.62 |
.53 |
.44 |
.33 |
.21 |
440C |
.50 |
.31 |
.27 |
.22 |
.17 |
.11 |
DR/ES1 |
.8 |
.49 |
.42 |
.35 |
.27 |
.17 |
|
a2 = Life correction factor for operating conditions. It has been empirically determined to have a value between 2.0 under ideal operating conditions and 0.2 where one or more of the following conditions may apply:
- The lubricant film thickness between the raceways and the rolling elements is low
- Bearing raceways are excessively misaligned
- Oscillatory motion
- Rotation speed of the bearing elements is very low
- Contamination or water is present in the bearing
Since there are many factors that determine observed bearing life, the above figures should be used conservatively. |
| MAXIMUM STATIC LOAD Co |
When subjected to an excessive load or shock, rolling bearings may incur a permanent damage to the raceways, called brinelling. This occurs when the elastic limit of the raceway material is exceeded and will permanently effect the smooth rotation of the bearing.
The maximum static load rating of a bearing (Co) is defined as that load which will produce a contact stress of 609,000 lbf /in2 (428 kgf/mm2) between the rolling element (ball) and the raceway. The values of Co are listed in the bearing tables for each individual bearing. Exceeding this value will damage the bearing. |
| EQUIVALENT DYNAMIC LOAD |
P = Pr + Pa |
where: |
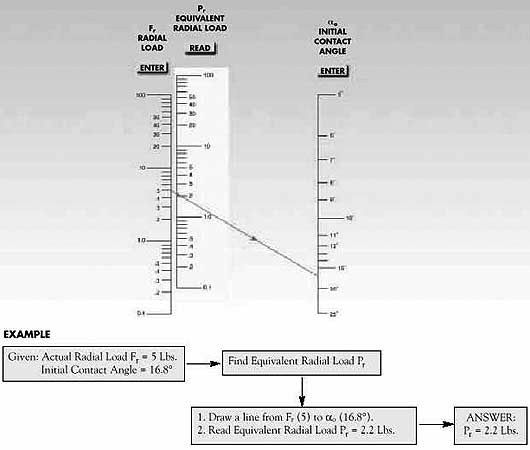
Pr , Pa are equivalent radial and axial equivalent loads, calculated using the nomographs on the next pages. |
|
| EQUIVALENT RADIAL LOAD NOMOGRAPGH (LBS. OR KG) |
 |
| PREDICTED BEARING LIFE |
| Based on the previous discussion, the following steps should be taken to calculate estimated real-world bearing life in revolutions x 106: |
| BEARING LIFE CALCULATION |
1. |
Obtain C and Co Load ratings for chosen bearing individual tables |
2. |
Radial play gives αo initial contact angle from formula or chart |
3. |
Input actual loads Fr, Fa into nomographs to determine equivalent loads Pr, Pa. |
4. |
Use P = Pr + Pa in basic L10 formula, derating C for high temperature, if necessary |
5. |
Apply general correction factors according to material and operating environment |
|



